FUNCIONES INVERSAS

FUNCIONES INVERSAS

Las funciones inversas, en un sentido más amplio, son las funciones que hacen lo "contrario" de otra.
 La notación f –1 se refiere a la inversa de la función f y no al expone -1 usado para números reales. Únicamente se usa como notación de la función inversa. 

Se llama función inversa o recíproca de f a otra función f –1  que cumple con: 

 f(a)= b, entonces f –1 (b)= a.

Se puede deducir que el dominio de f –1 es el recorrido de f, y que el recorrido de f –1 es el dominio de f. Entonces si hacemos la inversa de la inversa de una función, obtenemos la función inicial.
La función inversa no siempre existe, y cuando existe es única. La inversa de una función existe siempre y cuando la función inicial sea biyectiva.

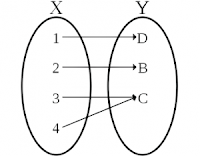
Una función biyectiva es cuando la función es inyectiva y sobreyectiva, es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.

• Una función es inyectiva si los elementos distintos del conjunto de salida (dominio), también conocido como conjunto "x", les corresponden elementos distintos del conjunto de llegada (codominio), conocido como "y". 

• Una función es sobreyectiva si cada elemento del conjunto de y es imagen de como mínimo un elemento del conjunto x.

A que resaltar que, para que una función f posea inversa es necesario que sea biyectiva. Y por lo tanto, las funciones trigonométricas al no ser inyectivas por su dominio, no poseen inversa. Pero si restringimos el dominio, obtendremos funciones inyectivas.
La inversa de una función trigonométrica se denomina función arco.