Lunes,17 de diciembre de 2018
Valeria Sandoval Sotomayor.
Grado décimo.
Física.

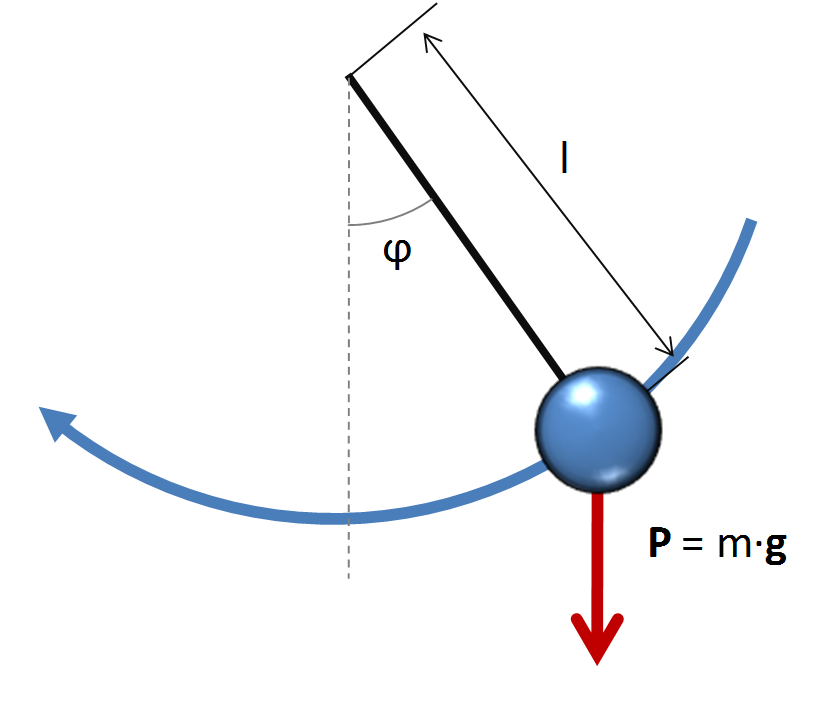
 PÉNDULO SIMPLE 

En la mesa redonda se tocaron puntos claves sobre ciertos aspectos desconocidos sobre el péndulo:

• ¿Que es el punto de deformación de un resorte?

         Cuando el resorte se estira mucho su forma cambia,por lo tanto su constante de elongación                   también,al igual que su posición de equilibrio.

• Para que el péndulo esté confinado en una sola dimensión,las oscilaciones no dependen mi de la amplitud de la masa,depende de la gravedad y la longitud del cable.
• ¿En que momento la ley de Hooke no funciona?

        Cuando una de las vueltas del resorte roza a la otra y cuando el resorte llegue al punto de                      deformación.

PÉNDULO SIMPLE

PÉNDULO SIMPLE

El péndulo simple es un objeto (una masa)  que pende de una cuerda, hilo o varilla( un objeto alargado cuya masa sea despreciable) 

Es un sistema oscilante, en el que tras ejercer una fuerza sobre el objeto, este, al  llegar a la cresta de su movimiento ondulatorio, se devuelve  con una fuerza igual a la inicial. 

VARIABLES DEL PÉNDULO

En el movimiento pendular intervienen 5 variables:

F: Fuerza del movimiento
m: Masa
L : Longitud de la cuerda
g: Gravedad
X: Distancia recorrida

A partir de estas variables podemos concluir una fórmula :

F= (m.g/L) X

En la que podemos encontrar la fuerza del movimiento al dividir el peso (masa multiplicada por la gravedad) entre la longitud de la cuerda que suspende la masa y multiplicar el valor obtenido por la distancia recorrida en el movimiento.
Y de esta manera, reemplazando variables podemos encontrar la variable necesitada


WEBGRAFIA
http://www.sc.ehu.es/sbweb/fisica/dinamica/trabajo/pendulo/pendulo.htm
http://hyperphysics.phy-astr.gsu.edu/hbasees/pend.html




Santiago Lasso Celis
Lunes, 17 de diciembre de 2018
Décimo 
Física      

PÉNDULO SIMPLE - MESA REDONDA

PÉNDULO SIMPLE

Un péndulo simple se define como una partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable.

Un péndulo simple es un ejemplo de oscilador no lineal. Se puede aproximar a un oscilador lineal cuando su amplitud es pequeña.

ECUACIONES DEL MOVIMIENTO

Si la partícula se desplaza a una posición θ₀ (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar.

El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Estudiaremos su movimiento en la dirección tangencial y en la dirección normal.

Las fuerzas que actúan sobre la partícula de masa m son dos

• el peso mg
• La tensión T del hilo

Descomponemos el peso en la acción simultánea de dos componentes, mg·sinθ  en la dirección tangencial y mg·cosθ en la dirección radial.

MOVIMIENTO ARMÓNICO SIMPLE 

El movimiento armónico simple (M.A.S.), también denominado movimiento vibratorio armónico simple (m.v.a.s.), es un movimiento periódico, y vibratorio en ausencia de fricción, producido por la acción de una fuerza recuperadora que es directamente proporcional a la posición, y que queda descrito en función del tiempo por una función trigonométrica (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s.

En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.

PÉNDULO SIMPLE

EL PÉNDULO SIMPLE

Se puede considerar como una masa puntual suspendida de una cuerda o varilla de masa despreciable. es un un sistema resonante con una frecuencia resonante.

Un sistema resonante es aquel al que se le aplica una pequeña carga (fuerza) con una frecuencia igual (o armónica) en fase a su frecuencia propia de oscilación, de modo que esa fuerza lo mantiene en oscilación y/o incrementa su período.

• Un péndulo simple es un ejemplo de oscilador no lineal. Se puede aproximar a un oscilador lineal cuando su amplitud es pequeña.

Galileo y los péndulos:

Sean Carroll relata la historia del descubrimiento de Galileo sobre el hecho de que para pequeñas amplitudes, el período y la frecuencia no se ven afectados por la amplitud. "Según se informa, en 1581, un joven Galileo Galilei hizo un descubrimiento revolucionario mientras estaba sentado y aburrido durante un servicio religioso en una iglesia de Pisa. La araña que pendía del techo sobre su cabeza, oscilaba suavemente hacia atrás y hacia delante, pero parecía moverse más rápidamente cuando el balanceo era más amplio (por ejemplo, después de una ráfaga de viento), y más lentamente cuando el balanceo era más corto. Intrigado, Galileo decidió medir el tiempo que duraba cada oscilación, utilizando para ello el único evento aproximadamente periódico al que tenia fácil acceso: los latidos de su propio pulso. Encontró algo interesante: el número de latidos del corazón entre los vaivenes de la araña era más o menos el mismo, independientemente de si las oscilaciones eran anchas o estrechas. El tamaño de las oscilaciones - la amplitud del recorrido del péndulo hacia adelante y hacia atrás-, no afectaba a la frecuencia de estas oscilaciones.

WEBGRAFIA

http://www.sc.ehu.es/sbweb/fisica/dinamica/trabajo/pendulo/pendulo.htm

http://hyperphysics.phy-astr.gsu.edu/hbasees/pend.html

PÉNDULO SIMPLE- MESA REDONDA

PÉNDULO SIMPLE 

Un péndulo simple es una masa suspendida en el extremo de una varilla, cuerda, hilo, cable o cordón de masa despreciable. El movimiento de un péndulo que se balancea de forma oscilante  a lo largo del arco de un circulo con igualdad de amplitud hacia cualquier lado de su punto de equilibrio, tiene una fricción despreciable. Sistema resonante con frecuencia resonante. Un péndulo simple es un ejemplo de oscilador no lineal.

Las oscilaciones de una péndulo no depende ni de la amplitud ni la masa, dependen de la gravedad y la longitud de la cuerda.

Para que un péndulo se mueva del reposo o punto de equilibrio, es necesaria de una fuerza extrema y su fórmula sería:

F= mg  x

       L                Siendo x la distancia recorrida.

La amplitud de cualquier péndulo en balanceo real disminuirá lentamente con el tiempo hasta que las oscilaciones de detengan por completo. A esto de le llama movimiento armónico amortiguado, y por lo general el amortiguamiento se debe a la resistencia del aire y a la fricción interna dentro del sistema en oscilación. 
Una  forma más teórica de explicar este movimiento sería, la energía que se disipa en energía térmica da como resultado una amplitud de oscilación disminuida. 

El movimiento armónico amortiguado se divide en tres sistemas, dependiendo de la ocasión. El primero es subamortiguamiento, es cuando se realiza varios balanceos antes de llegar al punto de equilibrio o reposo. El segundo es sobreamortiguamiento, es cuando toma mucho tiempo alcanzar el punto de equilibrio. Y el tercero es amortiguamiento crítico, en el cual el punto de equilibrio es alcanzado en un lapso de tiempo muy breve. 

DEBATE FUNCIONES INVERSAS 

FUNCIONES 

En matemáticas, una función f es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por: 

Una primera idea de función es la de una fórmula que relaciona algebraicamente varias magnitudes. 

La representación gráfica mediante diagramas cartesianos permite la visualización de las funciones. De este modo, el concepto de función se generaliza a cualquier relación numérica que responda a una gráfica sobre unos ejes coordenados.

FUNCIONES TRIGONOMÉTRICAS 

Las relaciones trigonométricas también pueden ser consideradas como funciones de una variable que es la medida de un ángulo.

Esta medida de ángulo puede ser dada en grados o radianes. Aquí, usaremos radianes. Ya que cualquier ángulo con una medida mayor que 2 π radianes o menor que 0 es equivalente a algún ángulo con medida 0 ≤ θ < 2 π , todas las funciones trigonométricas son periódicas. 

FUNCIONES INVERSAS 

En el sentido más amplio, son funciones que hacen lo “contrario” de cada una por ejemplo:

F convierte a en b por ende la inversa convierte b en a 

En otras palabras f(a)=b y f^-1(b)=a 

Para que una función tenga inversa debe ser inyectiva y sobreyectiva cosa que no vemos en las funciones trigonométricas y la pregunta es como seno, coseno, tangente, cotangente, secante y cosecante tienen función inversa, pues esto se logra restringiendo el dominio de la función logrando así obtener una función que aplique para la prueba de la línea horizontal y por ende tendrán inversa.

$\mathrm{<br>}$

Lunes,10 de diciembre de 2018
Valeria Sandoval Sotomayor.
Grado décimo.
Matemáticas.

DEBATE DE FUNCIONES INVERSAS 

En el debate se discutió de manera amplia el tema,descubriendo diferentes puntos que nunca antes se habían visto:

• Las funciones sobreyectivas a la vez son inyectivas debido a que tocan mínimo en un punto,aparte no se puede afirmar que una función que no es sobreyectiva,es inyectiva ya que por ende no existiría el concepto de una función biyectiva,la cual incluye a estas dos funciones.

FUNCIÓN INYECTIVA 

∀a,b∈Domf , si f(a)= f(b)⇒a=b

FUNCIÓN SOBREYECTIVA 

∀y∈Codf ∃x∈Domf / f(x)=y 

     

• También se comentó el porqué se le hacia una restricción a la función seno,como ejemplo puntual,luego de varias discusiones se concluyó que esto hacia parte del concepto de función,el cual no puede tocar más de dos puntos si se le traza una linea.

 

FUNCIONES INVERSAS

FUNCIONES INVERSAS

Se llama función inversa o recíproca de una función f a una nueva función cuyo dominio es la imagen de la función inicial, y su imagen es el dominio de la función inicial.

Es decir, si la función g es la función inversa de f, entonces se cumple que si f (b) = a, entonces g(a)=b.

El dominio de una función f(x) es el conjunto de todos los valores para los cuales la función está definida, y el rango de la función es el conjunto de todos los valores que f toma.

NOTA: Es función cuando todos los elementos del conjunto de salida tienen 1 y solo 1 imagen en el conjunto de llegada.

Si un elemento del conjunto de salida tiene mas de una imagen no es función, si un elemento del conjunto de salida no tiene imagen no es función.

FUNCIÓN INYECTIVA

La función f es inyectiva si cada elemento del conjunto final y tiene como máximo un elemento del conjunto inicial x al que se corresponde. Es decir, no puede haber más de un valor de x que tenga la misma imagen y.

FUNCIÓN SOBREYECTIVA

Una función es sobreyectiva si cada elemento del conjunto de llegada corresponde por lo menos a un elemento del conjunto de partida. 

Rango= Conjunto de llegada.

Rango= {D,B,C}

Conjunto de llegada = {D,B,C}

Por lo tanto es una función sobreyectiva.

Lunes, 10 de diciembre de 2018

Nombre: Alejandra Vargas Hoyos.

Área: Matemáticas.

Grado: Décimo.

FUNCIONES INVERSAS - FRANCISCO RAMIREZ DUEÑAS

FUNCIONES INVERSAS

Las funciones inversas nos permiten descubrir algunas características de las aplicaciones o su función. En esta se pueden explorar representaciones simbólicas o gráficas, o evaluar diversas características como el dominio o rango de una función.

En las funciones inversas podemos encontrar las biyectivas, inyectivas y sobreyectivas. A continuación profundizare acerca de estas.

BIYECTIVAS:

Una función es biyectiva si es inyectiva y sobreyectiva. En tal caso, existe una función g, llamada función inversa, tal que para todo x del dominio,

y para todo y de la imagen Normalmente, la función inversa de  se denota por en lugar de .

INYECTIVAS:

Una función es inyectiva si para todo x e y distintos de X sus imágenes f(x) y f(y) son distintas. Es decir, una función es inyectiva cuando las imágenes de elementos distintos son distintas.

dada una función cualquiera, buscando un adecuado subconjunto del dominio donde ella sea inyectiva, se puede obtener una inversa.

SOBREYECTIVAS:

Una función es sobreyctiva (o suprayectiva) si todos los elementos de la imagen, Y tienen anti-imagen. Es decir, si para cualquier y de la imagen Y existe al menos un elemento x de la imagen tal que f(x) = y. Una función es biyectiva si es inyectiva y sobreyectiva. En tal caso, existe una función g, llamada función inversa, tal que para todo x del dominio.

DEBATE FUNCIÓN INVERSA

DEBATE FUNCIÓN INVERSA

Primera intervención del debate realizada por David Medina:

Se llama función inversa o reciproca de F a otra función F^-1

que cumple que :   si F(a)= b , entonces F^-1(b)=a 

Entonces la notación F^-1 se refiere a la inversa de la función f y no al exponente -1 usado para números reales. únicamente se usa como notación para la función inversa.

cumpliendo así las siguientes propiedades:

1. la inversa de una función cuando existe es única. 
2. La inversa de una función cualquiera no siempre existe.
3. la inversa de una función biyectiva siempre existe.
4. las gráficas de las funciones F^-1 y F son simétricas respecto a la función identidad y=x.

sabiendo esto entonces podemos hallar que:

g(f(x)= g (2x)               f(g(x))=f(x/2)

        = 2x/2                           =2(x/2)

        = x                                =x

De esta manera se puede decir que las funciones que multiplicas por 2 y la función que divides por dos son lo contrario una de otra.

Por lo tanto la gráfica f^-1 se obtiene de la gráfica f de voltear sobre la recta y=x , a través de 180°.
Resultando que el dominio de f^-1es el mismo que el rango de f, y viceversa.

Dato importante sobre el debate:

sobreyectiva es aquella en la que su minimo es 1

x≥1 o 1≤x

inyectiva: su máximo es 1

x≤1 o 1≥x